Process of elimination
One very familiar strategy to anyone who has ever taken a multiple choice exam is process of elimination.
Example 1
In the game Sudoku, the objective is to fill in the empty spaces in a Sudoku board with numbers between \(1\) and \(9\). A Sudoku board consists of a \(3\times 3\) grid of blocks, where each block is further composed of a subgrid of \(3\times 3\) entries. The goal is to choose entries so that each number occurs exactly one time in each row, column and \(3\times 3\) block.
Problem: Determine the value of the entry in the center of the center-right \(3\times 3\) block of the following Sudoku board.
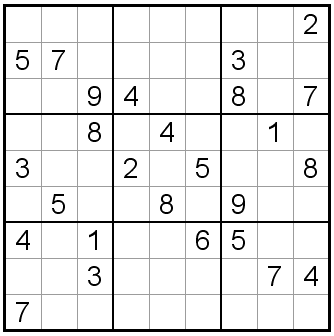
We know that the entry should be \(1,2,3,4,5,6,7,8,\) or \(9\). Since the center-right \(3\times 3\) block already has \(1,8,\) and \(9\), we can eliminate those. Also the same row has a \(2,3,\) and \(5\) and the column has a \(7\), so we can eliminate those as well.
Thus we are left with the entry being either \(4\) or \(6\).
If the entry is \(4\), then that forces the upper left entry of the upper right block to be \(4\), and therefore the center right entry of the upper left block is \(4\). However, this means that the lower left entry of the center left block must be \(4\). However, that puts two \(4\)’s in the far left column!
Thus we have eliminated \(4\) and the only possible value for the entry in the center of the center right block is \(6\).