Introduction to Graphs

A graph is a mathematical construction consisting of a collection of little round spots called vertices connected together by straight lines called edges. It turns out that graphs are a very natural and wonderful way of representing numerous real-world phenomena, including electrical networks, social networks, complicated atomic structures, and biological data.

The Konigsberg Bridge Problem

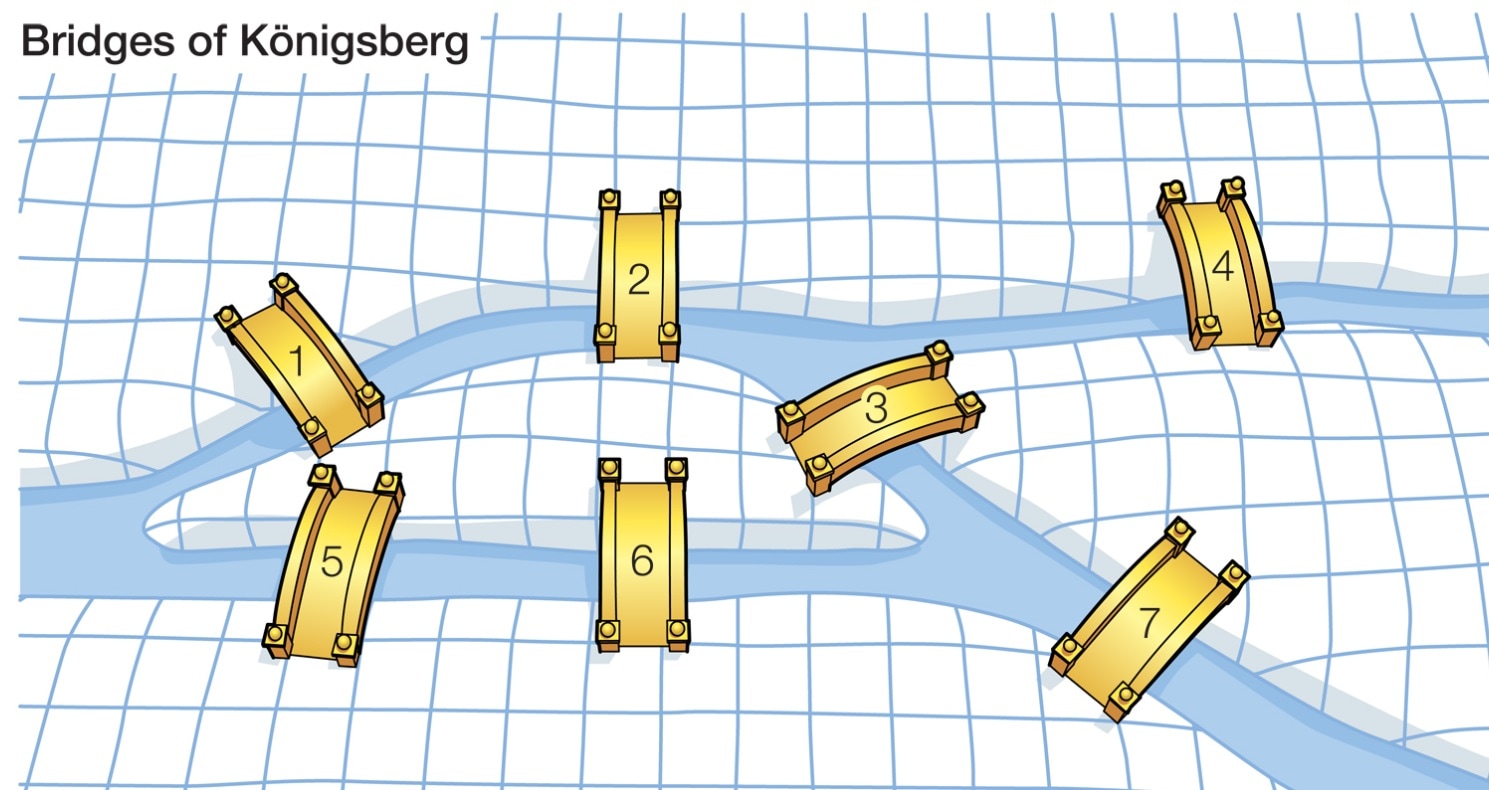
In the picture above, we have a cartoon version of a very famous problem solved by Euler in 1736. The question he answered is the following.

Is there a way to cross every single bridge in Konigsberg without crossing any bridge more than once?

In order to analyze this problem, Euler visualized this problem as a graph theory problem. He let the various bodies of land be represented by vertices, where the bridges are connected by edges. This produces a graph consisting of four vertices and seven edges as pictured below.

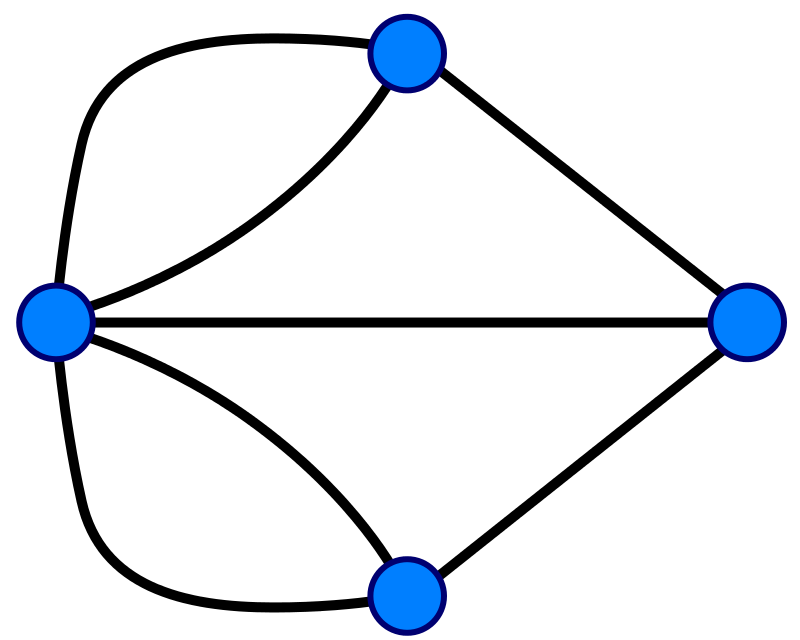
Each vertex (the blue circles) represents one of the land masses in the picture above. The edges each correspond to a bridge. For this reason, this particular graph is often called the Konigsberg graph. The problem then is to find a path on the Konigsberg graph which crosses every single edge once and only once. Nowadays, paths on graphs which pass through every edge exactly one time are called Eulerian paths.

Solving the Konigsberg Bridge Problem

To solve the Konigsberg bridge problem, Euler imagined travelling on a path on the Konigsberg graph which traveled across every edge exactly one time. He realized that on such a path, except for possibly the vertices that the path begins and ends on, every time he entered a vertex he would have to leave again by a different edge then the one he came in on. Therefore for all but possibly two of the vertices, there should be an even number of edges touching each vertex! The Konigsberg graph has more than two vertices with an odd number of edges, so it cannot have such a path. Thus there is no such desirable path through the city of Konigsberg!

Using Graphs in Micro Robots

Graphs provide us with a natural way to study the game Micro Robots. Think for example about the following Micro Robots board.

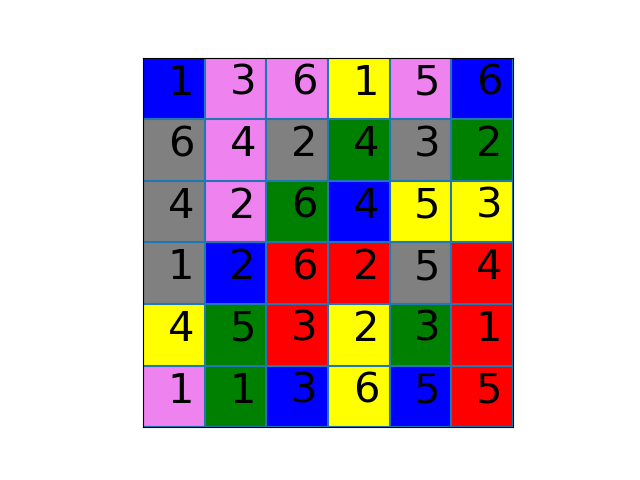
Let's try to answer the following question.

Is there a way for the robot to move from the Violet 4 square to the Yellow 3 square while passing through Yellow 6?

A solution seems very tricky! After trying for a while and failing, we might even be convinced that there isn't one. However, by understanding the game board as a graph, we can make much better progress!

We think of each colored box as a vertex, obtaining a total of 36 vertices. Then we create a graph by connecting two vertices with an edge when the robot can move between the corresponding boxes in a single move. In other words, vertices are connected when both of the following conditions are satisfied

the corresponding boxes are in the same row or column
the corresponding boxes have the same color or number

For the game board above, this produces the following graph.

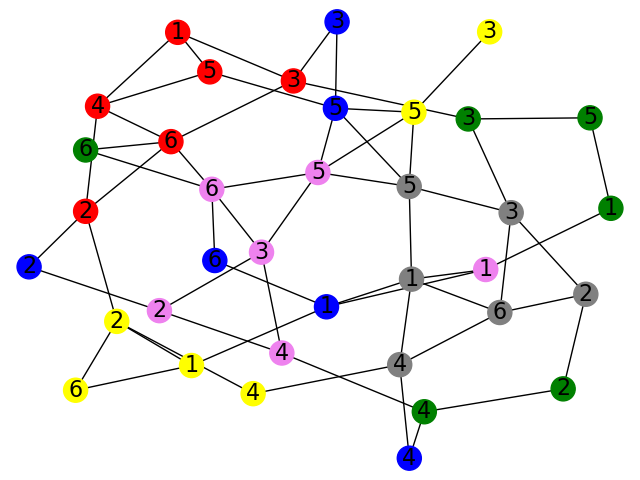
Here, we have labelled the vertices according to the colored boxes that they correspond to in the board. This graph version of the board is extremely useful, since it allows me to answer some otherwise complicated questions very simply. For example, from this view we see we can move in the following way to go from the Violet 4 square to the Yellow 3 square while passing through Yellow 6 in between:

Violet 4 $LaTeX: \rightarrow$ Violet 3 $LaTeX: \rightarrow$ Violet 2 $LaTeX: \rightarrow$ Blue 2 $LaTeX: \rightarrow$ Red 2 $LaTeX: \rightarrow$ Yellow 2 $LaTeX: \rightarrow$ Yellow 6 $LaTeX: \rightarrow$

Yellow 1 $LaTeX: \rightarrow$ Blue 1 $LaTeX: \rightarrow$ Gray 1 $LaTeX: \rightarrow$ Gray 3 $LaTeX: \rightarrow$ Gray 5 $LaTeX: \rightarrow$ Yellow 5 $LaTeX: \rightarrow$ Yellow 3

A very complicated path, but it exists!

Notice above that the graph is connected. This means there is always some path connecting any vertex to any other vertex. When the graph can be separated out into multiple different components that are not connected by any edges, the graph is called disconnected.

Some Interesting Questions

Here we reflect on some interesting questions that a bright student might think about on a nice, sunny day. You are not required to answer any of these unless otherwise stated.

Can any kind of graph with 36 vertices be made from some kind of Micro Robots game board? If not, what kinds of graphs can we make?
Is it possible to find a fixed Micro Robots game board whose corresponding graph is disconnected?
Is it possible to create a Micro Robots game board whose corresponding graph has an Eulerian path? What does this mean in terms of the board itself?