Cardinaltiy Homework 1
For this homework, we will rely on the following two definnitions.
Definition 1: A composition of a positive integer \(n\) is a sequence of integers \((a_1,a_2,\dots,a_k)\) all greater than \(0\) which add up to \(n\). The integer \(k>0\) is called the length of the composition.
Definition 2: A partition of a positive integer \(n\) is a composition \((a_1,a_2,\dots,a_k)\) of \(n\) satisfying \(a_1\geq a_2\geq\dots\geq a_k\).
For example, \((1,3,1)\) and \((3,1,1)\) are both compositions of \(5\), but only the second one is a partition.
Problem 1
Fill in the missing values in the following table. Make sure to carefully show your work.
| \(n\) | number of compositions | number of partitions |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 4 | 3 |
| 4 | ||
| 5 | 16 | |
| 6 |
Problem 2
Let \(A\) be the set of partitions of \(2021\) and let \(B\) be the set of composition of \(2021\). Which set has larger cardinality? Carefully explain.
Problem 3
- (A) List the partitions of \(25\) whose first entry is 20.
- (B) List the partitions of \(25\) whose length is 20.
Problem 4
Graphically, partitions can be represented by a Young diagrams. A young diagram is a sequence of empty squares left-aligned on top of each other. For a partition \((a_1,a_2,\dots,a_k)\), the number of boxes in the \(j\)‘th row from the top is exactly \(a_j\).
Example: The Young diagram corresponding to the partition \((5,4,1)\) of \(10\) is

Example: The Young diagram corresponding to the partition \((5,3,1,1)\) of \(10\) is
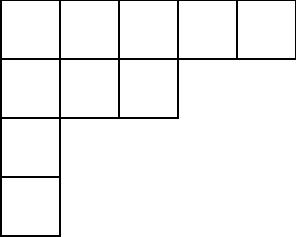
- (A) Draw the Young diagrams for all of the partitions of \(4\).
- (B) Draw the Young diagrams for all the partitions of \(10\) whose first entry is \(6\).
- (C) Draw the Young diagrams for all the partitions of \(10\) whose length is \(6\).
- (D) Can you find a relationship between the Young diagrams pictured in (B) and (C)?
Problem 5
Use Young diagrams to establish a bijection between the sets
\[A = \{x | \text{$x$ is a partition of $40$ of length $20$}\}\] \[B = \{x | \text{$x$ is a partition of $40$ whose first entry is $20$}\}\]This shows that \(A\) and \(B\) are the same size, even though we don’t know what that size actually is!