Microrobots Homework
A full Micro Robots board consists of four 3x3 cards which, when put together into a square, form a 6x6 grid. Each of the nine entries on a card has one of six colors and a number between one and six. Furthermore, when arranged into the full 6x6 grid, each color and number combination occurs exactly one time. For example, there will be exactly one red 4 tile and exactly one blue 2 tile.
Problem 1
Using the Micro Robots board shown below, we constructed the associated graph.
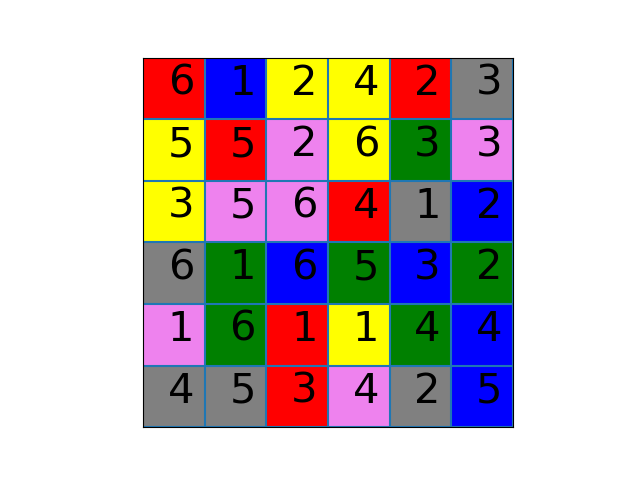
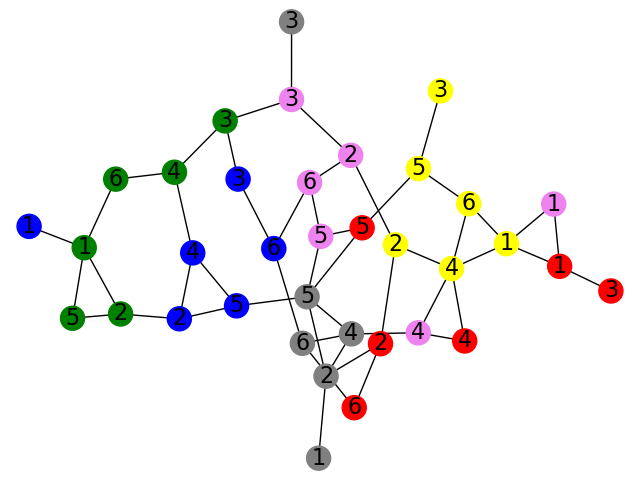
- What do the vertices of the graph correspond to?
- What about the edges?
-
-
- The graph is connected, so what does that tell us?
-
- If I wanted to make a round of the game as hard as possible, what squares would I choose for the robot’s starting point and the robots goal? Explain why your choice is the hardest.
- For the squares you indicated in your previous answer, what is the minimum number of moves required by the robot?
Problem 2
Create a fixed Micro Robots board (ignoring shuffling or rotation) where it is possible for the robot to get stuck: where for a certain starting point and ending goal, the robot will be unable to get to the goal from the start. Make sure that your board has each color and letter combination occurring exactly one time! Your solution should include
- A picture of the board
- An indication which starting point and end goal is not possible on your board
- A detailed explanation why the robot can’t make it to the goal
Problem 3
For the Micro Robots board you created in Problem 2, create a drawing of the associated graph. What property of the graph tells us that it is possible for the robot to get stuck?
Problem 4
Create a fixed Micro Robots board (ignoring shuffling or rotation) where the robot can move from any position to any other position in two or less moves. Explain in detail why you know that the robot is able to do this in your example.
Problem 5
Suppose somebody hands you four \(3\times 3\) cards which form a Micro Robots board.
- Determine the total number of possible ways that we can arrange the cards into a board. Don’t forget about rotations!
- Give an example of two different arrangements of the board that end up giving you the same graph.
- Determine how many of the different arrangements that you found in the previous part result in a distinct graphs.